于是,XSC062 开始写总结。
斜率优化 DP
前置芝士
正文
我们以一道题为例。
打印文章
Solution
明显 DP。
那么 DP 式就是: \[ \begin{aligned} f_i&=\min\{f_j+(s_i-s_j)^2+M\} \\ &=\min\{f_j+{s_i}^2-2\times s_i\times s_j+{s_j}^2+M\} \\ &=\min\{f_j-2\times s_i\times s_j+{s_j}^2\}+{s_i}^2+M \end{aligned} \] 其中 \(s\) 为 \(c\) 的前缀和。
时间复杂度 \(O(n^2)\),明显爆炸,所以我们需要优化。
在上一篇的 单调队列优化DP 中,我们提到过,只有 DP 式中的与 \(i\) 有关的项能直接提出来时,我们才能使用单调队列优化,而这里的 \(s_i\) 与 \(s_j\) 相乘,无法使用单调队列优化。
我们思考,对于 \(f_i\) 来说,无非就是选出最优的 \(j\) 来构造它。
假设有 \(j\) 与 \(k\),如何判断 \(j\) 与 \(k\) 谁更优呢?
我们先钦定 \(j\) 优于 \(k\),且 \(j<k\)。
那么可以得到: \[ f_j-2\times s_i\times s_j+{s_j}^2+{s_i}^2+M<f_k-2\times s_i\times s_k+{s_k}^2+{s_i}^2+M \] 化简得: \[ f_j-2\times s_i\times s_j+{s_j}^2<f_k-2\times s_i\times s_k+{s_k}^2 \] 再将只与 \(j,k\) 有关的项放到左边,与 \(i\) 有关的项放到右边: \[ f_j-f_k+{s_j}^2-{s_k}^2<2\times s_i\times s_j-2\times s_i\times s_k \\ f_j-f_k+{s_j}^2-{s_k}^2<2\times s_i\times(s_j-s_k) \] 左右两边同时 \(\div\) 与 \(i\) 无关的项 \(2\times(s_j-s_k)\) : \[ \dfrac{(f_j+{s_j}^2)-(f_k+{s_k}^2)}{(2\times s_j)-(2\times s_k)}<s_i \] 如果满足上式 ,则 \(j<k\) 且 \(j\) 优于 \(k\)。
接下来是斜率优化的重点部分。
在义务教育阶段,学生学习了 一次函数,它的几何意义表示为一条直线,一次项的系数就是直线的斜率,只不过当直线与 \(x\) 轴垂直的时候无法表示。虽然没有明确给出斜率这个名词,但实际上思想已经渗透到其中。
直线对 \(x\) 轴的倾斜角 \(\alpha\) 的正切值 \(\tan\alpha\) 称为该直线的“斜率”,并记作 \(k\) ,公式为 \(k=\tan\alpha\)。
即 \(k=\tan\alpha=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}\) 或 \(\dfrac{y_1-y_2}{x_1-x_2}\) 。
——选自 斜率_百度百科
XSC062 看完了百度百科表示 你 TM 在说些啥是不是欺负我六年义务教育的小学生 恍然大悟
上面推出来的那个关于 \(j\) 和 \(k\) 的DP式,不就是求两个点 \((2\times s_j,f_j+{s_j}^2)\) 和 \((2\times s_k,f_j+{s_k}^2)\) 连成一条线之后的坡度吗?
本文后面的部分,\(x\) 的含义会在「点\((2\times s_x,f_x+{s_x}^2)\) 」和「下标 \(x\) 」之间漂浮,请根据语境识别。
随后 XSC062 边打瞌睡边听 GM 讲课(特异功能),勉强算是明白了中心意思:
如图,假设有三个点 \(A,B,C\),以及 \(l_{AB}\) 的斜率 \(k_1\),\(l_{BC}\) 的斜率 \(k_2\)。
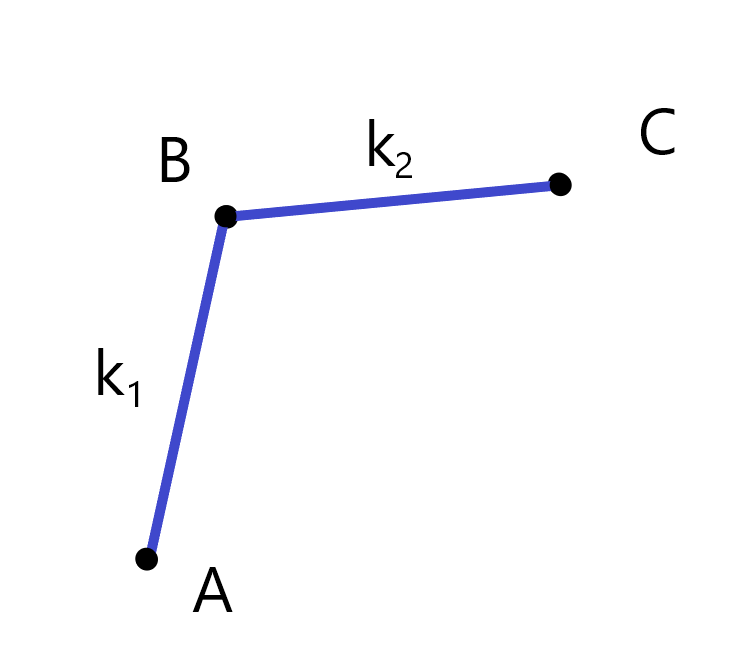
我们暂且把这个向外凸起的奇怪玩意儿称为一个「上凸」。
回到前面的我们得到的那个结论:
\[ \dfrac{(f_j+{s_j}^2)-(f_k+{s_k}^2)}{(2\times s_j)-(2\times s_k)}<s_i \]
如果满足上式 ,则 \(j<k\) 且 \(j\) 优于 \(k\)。
简单记忆为:
- 若 \(l_{NM}\) 的斜率比 \(s_i\) 小,则 \(N<M\) 且 \(N\) 优于 \(M\) 。
- 反之,若点 \(l_{NM}\) 的斜率比 \(s_i\) 大,则 \(M<N\) 且 \(M\) 优于 \(N\)。
将 \(A,B\) 代入,我们得知:
- 若 \(k_1\leqslant s_i\),则 \(B\) 优于 \(A\)。
- 若 \(k_1>s_i\),则 \(A\) 优于 \(B\)。
- 若 \(k_2\leqslant s_i\),则 \(C\) 优于 \(B\)。
- 若 \(k_2>s_i\),则 \(B\) 优于 \(C\)。
因为斜率 = 倾斜度 = 竖得有多高,明显 \(k_1>k_2\)。所以针对一个大小关系,\(k_1\) 和 \(k_2\) 之间只有可能有:
- \(s_i<k_2<k_1\),此时 \(B\) 优于 \(C\),\(A\) 优于 \(B\),\(A\) 为最优解。
- \(k_2<s_i<k_1\),此时 \(C\) 优于 \(B\),\(A\) 优于 \(B\),\(A,C\) 为最优解。
- \(k_2<k_1<s_i\),此时 \(C\) 优于 \(B\),\(B\) 优于 \(A\),\(C\) 为最优解。
发现了吗?\(B\) 永远都不可能是最优解。
所以如果我们要维护一个最优解的序列,就可以不要 \(B\) 了。

那么,因为我们已经删掉了所有「上凸」的突起部分,所以这个最优解序列里肯定不会再存在「上凸」了。
如果是这样的「下凸」呢?

\(k_1\) 为 \(l_{AB}\) 的斜率,\(k_2\) 为 \(l_{BC}\) 的斜率。
将 \(A,B\) 代入,我们得知:
- 若 \(k_1\leqslant s_i\),则 \(B\) 优于 \(A\)。
- 若 \(k_1>s_i\),则 \(A\) 优于 \(B\)。
- 若 \(k_2\leqslant s_i\),则 \(C\) 优于 \(B\)。
- 若 \(k_2>s_i\),则 \(B\) 优于 \(C\)。
明显 \(k_1<k_2\)。所以 \(k_1\) 和 \(k_2\) 之间只有可能有:
- \(s_i<k_1<k_2\),此时 \(B\) 优于 \(C\),\(A\) 优于 \(B\),\(A\) 为最优解。
- \(k_1<s_i<k_2\),此时 \(B\) 优于 \(C\),\(B\) 优于 \(A\),\(B\) 为最优解。
- \(k_1<k_2<s_i\),此时 \(C\) 优于 \(B\),\(B\) 优于 \(A\),\(C\) 为最优解。
所以,在下凸的情况中,三个点都有可能是最优解,都需要保留。
现在呢,所有上凸都被去掉了,只剩下凸,所以大概最后的最优解序列就长这个样子:

下 秃 包
反过来看就是 lifan 的脑袋了
观察发现,斜率是从左往右递增的。
所以,我们考虑用单调队列来当这个「最优解序列」。
维护队头
即保证队头元素为最优解。
设队头为 \(q_l\)。
如果 \(q_{l+1}\) 与 \(q_l\) 形成的斜率 \(\leqslant s_i\),根据上面推出来的玩意儿,得到 \(q_{l+1}\) 优于 \(q_l\)。
那还要 \(q_l\) 干啥,直接 l++。
更新 DP 值
\(f_i=f_{q_l}-2\times s_i\times s_{q_l}+{s_{q_l}}^2+{s_i}^2+M\)
维护队尾
即保证里面塞的点相邻两个的斜率递增。
设队尾为 \(q_r\),我们要往最优解队列里 push 一个 \(i\) 。
若队尾两个点 \(q_r,q_{r-1}\) 形成的斜率比 \(i,q_r\) 形成的斜率大,那么push(i)后,整个队列的斜率就不再单调递增,所以此时要将r--。(因为 上一篇关于单调队列的博客 中讲到的 \(i\) 必须入队,只能委屈一下 \(q_r\) 了)
注意事项
众所周知,斜率是个浮点数。为了避免损失精度造成的一些惨案,我们交叉相乘,将分子、分母分开处理。
以及时刻都要保证队列中至少有两个点,因为要访问 \(q_l,q_{l+1}\) 和 \(q_r,q_{r-1}\)。
Code
#include <cstdio>
const int maxn = 5e5 + 5;
int n, m, l, r;
int f[maxn], c[maxn], q[maxn];
inline int getDP(int i, int j) {
return f[j] + m + (c[i] - c[j]) * (c[i] - c[j]);
}
inline int getup(int j, int k){
return f[j] + c[j] * c[j] - f[k] - c[k] * c[k]; // 计算分子的值
}
inline int getdown(int j, int k) {
return (c[j] - c[k]) * 2; // 计算分母的值
}
int main(){
while (~scanf("%d %d", &n, &m)) {
l = r = 1; // 凡是涉及到前缀和的单调队列,队列中必须存在初始 0
for (int i = 1; i <= n; ++i) {
scanf("%d", &c[i]); // c 自给自足
c[i] += c[i - 1];
// # 维护队头
// 注意此处的条件为 l < r,因为队列中至少需要存在两个点
while (l < r && getup(q[l+1], q[l]) <= c[i] * getdown(q[l + 1],q[l]))
l++;
// # 转移状态
f[i] = getDP(i, q[l]);
// # 维护队尾
while(l < r&& getup(i, q[r]) * getdown(q[r], q[r-1]) <= getup(q[r] ,q[r - 1]) * getdown(i, q[r]))
r--;
q[++r] = i;
}
printf("%d\n",f[n]);
}
return 0;
}在对 DP 式变形时,我们最好将其化为 \(\dfrac{(j)-(k)}{(j)-(k)}<x\) 或 \(\dfrac{(j)-(k)}{(j)-(k)}>x\) 的形式。
这个板子只适用于维护下凸包的情况。当中间的符号为 \(>\) 时,我们会在这份代码上稍作改动,维护一个上凸包,后文会提到有关内容。
玩具装箱
从今往后我们就只讲怎么推式子,不再证明下凸等性质了。
设 \(f_i\) 表示第 \(i\) 个玩具放完后的最小费用。 \[
f_i=\min\{f_j+(i-j-1+\sum\limits_{k=i}^jC_k-L)^2\}
\] 为了让这个式子好拆,我们在一开始让 l++,并且 \(C\) 再次自给自足,为输入的 \(C\) 的前缀和数组。
于是式子就变成: \[ f_i=\min\{f_j+(i-j-L+C_i-C_j)^2\} \] 明显硬拆会死人。(反正我试过,比较适合用来发泄
所以我们把式子变成这样: \[ f_i=\min\{f_j+((C_i+i)-(C_j+j)-L)^2\} \] 既然 \(C_i\) 与 \(i\),\(C_j\) 与 \(j\) 是对应的,那么直接预处理,给 \(C_i\) 加上 \(i\) 不就行了?
现在这个 \(C_i\) 的含义和实现就变得有点曲折难懂了。
具体实现如下:
for (int i = 1; i <= n; ++i) {
scanf("%lld", &c[i]);
c[i] += c[i - 1];
}
for (int i = 1; i <= n; ++i)
c[i] += i;也就是说,\(C_i\) 是在前缀和的基础上加了一个 \(i\),注意不能把 \(i\) 也一起前缀和了。
然后式子就变成了这样: \[ \begin{aligned} f_i&=\min\{f_j+(C_i-C_j-L)^2\} \\ &=\min\{f_j+{C_i}^2+{C_j}^2+L^2-2\times C_i\times C_j-2\times C_i\times L+2\times C_j\times L\} \\ &=\min\{f_j+{C_j}^2-2\times C_i\times C_j+2\times C_j\times L\}+{C_i}^2+L^2-2\times C_i\times L \end{aligned} \]
令 \(j\) 优于 \(k\) 且 \(j<k\)。
得: \[ f_j+{C_j}^2-2\times C_i\times C_j+2\times C_j\times L<f_k+{C_k}^2-2\times C_i\times C_k+2\times C_k\times L \\ f_j-f_k+{C_j}^2-{C_k}^2+2\times C_j\times L-2\times C_k\times L<2\times C_i\times C_j-2\times C_i\times C_k \\ f_j-f_k+{C_j}^2-{C_k}^2+2\times C_j\times L-2\times C_k\times L<2\times(C_j-C_k)\times C_i \\ \dfrac{f_j-f_k+{C_j}^2-{C_k}^2}{2\times(C_j-C_k)}<C_i \\ \dfrac{(f_j+{C_j}^2)-(f_k+{C_k}^2)}{(2\times C_j)-(2\times C_k)}<C_i \]
#include <cstdio>
#define int long long
const int maxn = 5e5 + 5;
const int LEN = (1 << 20);
int n, m, h, t;
int c[maxn], q[maxn], f[maxn];
#define nec getchar
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1; ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
inline int getup(int j, int k) {
return (f[j] + c[j] * c[j] + 2 * c[j] * m)
- (f[k] + c[k] * c[k] + 2 * c[k] * m);
}
inline int getdown(int j, int k) {
return (2 * c[j]) - (2 * c[k]);
}
inline int getDP(int i, int j) {
return f[j] + (c[i] - c[j] - m) * (c[i] - c[j] - m);
}
signed main() {
read(n); read(m); h = t = 1; ++m;
for (int i = 1; i <= n; ++i)
read(c[i]), c[i] += c[i - 1];
for (int i = 1; i <= n; ++i) {
c[i] += i;
while (h < t && getup(q[h + 1], q[h]) <
c[i] * getdown(q[h + 1], q[h])) ++h;
f[i] = getDP(i, q[h]);
while (h < t
&& getup(i, q[t]) * getdown(q[t], q[t - 1]) <=
getdown(i, q[t]) * getup(q[t], q[t - 1])) --t;
q[++t] = i;
}
printf("%lld", f[n]);
return 0;
}任务安排 1
感谢蓝书。这里按着蓝书上的思维走。
解法一
暴力。
此处的 \(t,c\) 为输入的 \(t,c\) 的前缀和数组。
设 \(f_{i,j}\) 为前 \(i\) 个任务分成 \(j\) 批的最小费用。
故 \(S\times j+t_i\) 为第 \(i\) 个任务的完成时间。
得出状态转移方程(\(k\) 枚举上一批任务结束位置): \[ f_{i,j}=\min\limits_{0\leqslant k<i}\{f_{k,j-1}+(S\times j+t_i)\times(c_i-c_k)\} \] 时间复杂度 \(O(n^3)\)。
#include <cstdio>
#include <cstring>
#define int long long
const int inf = 1e18;
const int maxn = 5005;
const int LEN = (1 << 20);
int f[maxn][maxn];
int n, s, ans = inf;
int t[maxn], c[maxn];
inline int min(int x, int y) { return x < y ? x : y; }
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
signed main() {
read(n); read(s);
memset(f, 0x3f, sizeof (f));
for (int i = 1; i <= n; ++i) {
read(t[i]); read(c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
f[i][1] = (s + t[i]) * c[i]; // 初始化
}
for (int i = 2; i <= n; ++i) {
for (int j = 2; j <= i; ++j) {
for (int k = 1; k < i; ++k)
f[i][j] = min(f[i][j], f[k][j - 1] + (t[i] + s * j) * (c[i] - c[k]));
}
}
for (int i = 1; i <= n; ++i)
ans = min(ans, f[n][i]);
printf("%lld", ans);
return 0;
}亲测 TLE 70
解法二
脑子炸了,想了好久才想明白这个优化的正确性。
思考,以上代码需要 \(j\) 这一维的根本原因是什么?
因为我们无法确定之前已经划分了多少批,也就是无法确定 \(S\) 的个数。
换个角度思考,我们无法确定之前,却可以确定之后。
什么意思呢?如果我们在任务 \(i\) 处划分,那么任务 \(i\) 以及任务 \(i\) 以后的所有任务的执行时间都会延后 \(S\)。
因为 \(i\) 以后的状态也会使用 \(f_i\) 的值,我们在计算 \(f_i\) 时就将 \(S\) 提出来,提前把后面的 \(c\) 乘上不就行了?
中间的结果不对劲也无所谓,只要最后的答案是对的就行了。
也就是说,我们没有直接求出每批任务的完成时刻,而是在一批任务「开始」对后续任务产生影响时,就先把费用累加到答案中。这是一种名为「费用提前计算」的经典思想。
——李煜东《算法竞赛进阶指南》
状态转移方程: \[ f_i=\min\limits_{0\leqslant j<i}\{f_j+(c_i-c_j)\times t_i+s\times(c_n-c_j)\} \] 此处,\(f_i\) 没有具体含义。
#include <cstdio>
#include <cstring>
#define int long long
const int maxn = 1e4 + 5;
const int LEN = (1 << 20);
int n, s;
int f[maxn], t[maxn], c[maxn];
inline int min(int x, int y) { return x < y ? x : y; }
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
signed main() {
read(n); read(s);
memset(f, 0x3f, sizeof (f));
for (int i = 1; i <= n; ++i) {
read(t[i]); read(c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
f[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j)
f[i] = min(f[i], f[j] + t[i]* (c[i] - c[j]) + s * (c[n] - c[j]));
}
printf("%lld", f[n]);
return 0;
}任务安排 2
\(n\) 的范围变大了,\(n^2\) 过不了。
这不随手加个斜率优化的事儿吗。
我们继续瞎搞这个式子。 \[ \begin{aligned} f_i&=\min\{f_j+(c_i-c_j)\times t_i+s\times(c_n-c_j)\} \\ &=\min\{f_j+c_i\times t_i-c_j\times t_i+s\times c_n-s\times c_j\} \\ &=\min\{f_j-c_j\times t_i-s\times c_j\}+c_i\times t_i+s\times c_n \end{aligned} \] 令 \(j\) 优于 \(k\) 且 \(j<k\) 。
则有: \[ f_j-c_j\times t_i-s\times c_j<f_k-c_k\times t_i-s\times c_k \\ f_j-f_k-s\times c_j+s\times c_k<c_j\times t_i-c_k\times t_i \\ f_j-f_k-s\times c_j+s\times c_k<t_i\times(c_j-c_k) \\ \dfrac{(f_j-s\times c_j)-(f_k-s\times c_k)}{(c_j)-(c_k)}<t_i \] 然后就是老套路。
时间复杂度 \(O(n)\)。
#include <cstdio>
#define int long long
const int maxn = 5e5 + 5;
const int LEN = (1 << 20);
int n, s, L, R;
int f[maxn], t[maxn], c[maxn], q[maxn];
#define nec getchar
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1; ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
inline int getup(int j, int k) { return (f[j] - s * c[j]) - (f[k] - s * c[k]); }
inline int getdown(int j, int k) { return (c[j]) - (c[k]); }
inline int getDP(int i, int j) { return f[j] + (c[i] - c[j]) * t[i] + s * (c[n] - c[j]); }
signed main() {
read(n); read(s);
L = R = 1;
for (int i = 1; i <= n; ++i) {
read(t[i]); read(c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
for (int i = 1; i <= n; ++i) {
while (L < R && getup(q[L + 1], q[L]) <= t[i] * getdown(q[L + 1], q[L]))
++L;
f[i] = getDP(i, q[L]);
while (L < R && getup(i, q[R]) * getdown(q[R], q[R - 1]) <= getdown(i, q[R]) * getup(q[R], q[R - 1]))
--R;
q[++R] = i;
}
printf("%lld", f[n]);
return 0;
}任务安排 3
注意 \(t\) 有可能是负数。
\(t\) (输入)有可能为负,代表着 \(t\)(前缀和)不再单调递增,用不单调的对象作为单调队列的条件一看就十分不讲武德,这样维护出来的队头显然不是正确答案。
后面的 \(t,c\) 默认为前缀和。
我们感性证明一下。
一个最普通的例子,假设输入了一个负数,导致 \(t_i<t_{i-1}\),且有一斜率 \(>t_i\) 且 \(<t_{i-1}\)。
那么在 \(i-1\) 时,它就被维护队头的操作剔掉了,但也许它凑巧就是 \(i\) 的最优解,呜呼哀哉。
于是我们不能删队头元素了。那怎么查询最优解呢?
单调队列里装的始终还是个具有单调性的下凸包,于是我们可以在队列中二分一个 \(pos\),\(pos\) 与 \(pos-1\) 形成的斜率比 \(t_i\) 小,\(pos+1\) 与 \(pos\) 形成的斜率比 \(t_i\) 大。
然后把 \(pos\) 当成 \(q_l\) 来处理就好了。
队尾还是维护一个下凸。
时间复杂度 \(O(n\log n)\)。
强烈建议不要去动 AcWing 版本的那道。
最后两组数据堪称毒瘤。
卡 long long 乘法,卡 __int128 时限,卡 double精度,非 T 即 WA。
反正我搞了半个小时硬是没有搞出来。
#include <cstdio>
#define int long long
const int maxn = 3e5 + 5;
const int LEN = (1 << 20);
int n, s, L, R;
int f[maxn], t[maxn], c[maxn], q[maxn];
#define nec getchar
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1; ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
inline int getup(int j, int k) { return (f[j] - s * c[j]) - (f[k] - s * c[k]); }
inline int getdown(int j, int k) { return (c[j]) - (c[k]); }
inline int getDP(int i, int j) { return f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]); }
inline int Func(int u) {
if (L == R) return q[L];
int l = L, r = R;
while (l < r) {
int mid = l + r >> 1;
if (getup(q[mid + 1], q[mid]) <= u * getdown(q[mid + 1], q[mid]))
l = mid + 1;
else r = mid;
}
return l;
}
signed main() {
read(n); read(s);
L = R = 1;
for (int i = 1; i <= n; ++i) {
read(t[i]); read(c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
for (int i = 1; i <= n; ++i) {
int Best = Func(t[i]);
f[i] = getDP(i, q[Best]);
while (L < R && getup(i, q[R]) * getdown(q[R], q[R - 1]) <= getdown(i, q[R]) * getup(q[R], q[R - 1]))
--R;
q[++R] = i;
}
printf("%lld", f[n]);
return 0;
}土地购买
首先我们想明白一件事情:如果一块土地,有另一块土地的长和宽都比它大,那就不用再理它了,直接从总序列里剔除。
struct _ {
int w, l;
bool operator< (const _ q) const {
return w == q.w ? l > q.l : w > q.w;
}
} a[maxn];
...
std::sort(a + 1, a + n + 1);
for (int i = 1; i <= n; ++i) {
if (a[i].l > a[cnt].l)
a[++cnt] = a[i];
}然后就推式子。
贪心地想,在前面的操作后,\(a\) 是一个 \(w\) 递减,\(l\) 递增的土地序列。
所以我们选择将连续的一段区间分为一组,这样的话,一个组里的一段连续的土地 \([x,y]\) 就只有 \(w_x\) 和 \(l_y\) 起了作用,又没有中间那一段的事了。
设 \(f_i\) 表示分配完第 \(i\) 块土地后的最小花费。
则有: \[ f_i=\min\{f_j+w_{j+1}\times l_i\} \] 令 \(j\) 优于 \(k\)。
则有: \[ f_j+w_{j+1}\times l_i<f_k+w_{k+1}\times l_i \\ f_j-f_k<(-w_{j+1}+w_{k+1})\times l_i \\ \dfrac{(f_j)-(f_k)}{(-w_{j+1})+(w_{k+1})}<l_i \]
#include <cstdio>
#include <algorithm>
#define int long long
const int maxn = 5e4 + 5;
struct _ {
int w, l;
bool operator< (const _ q) const{
return w == q.w ? l > q.l : w > q.w;
}
};
_ a[maxn];
int n, cnt, l, r;
int q[maxn], f[maxn];
int getup(int j, int k) { return f[j] - f[k]; }
int getdown(int j,int k) { return a[k + 1].w - a[j + 1].w; }
int getDP(int i,int j) { return f[j] + a[j + 1].w * a[i].l; }
signed main() {
scanf("%lld", &n);
for(int i = 1; i <= n; ++i)
scanf("%lld %lld", &a[i].w, &a[i].l);
std::sort(a + 1, a + n + 1);
for (int i = 1; i <= n; ++i) {
if (a[i].l > a[cnt].l)
a[++cnt] = a[i];
}
n = cnt; l = r = 1;
for (int i = 1; i <= n; ++i) {
while (l < r && getup(q[l + 1], q[l]) <= a[i].l * getdown(q[l + 1], q[l]))
l++;
f[i] = getDP(i, q[l]);
while (l < r && getup(i, q[r]) * getdown(q[r], q[r - 1]) <= getup(q[r],q[r - 1]) * getdown(i, q[r]))
r--;
q[++r] = i;
}
printf("%lld", f[n]);
return 0;
}仓库建设
设 \(f_i\) 表示在 \(i\) 工厂建立仓库的最小花费。
则有: \[ \begin{aligned} f_i&=\min\{f_j+\sum\limits_{k=j+1}^{i-1}[(x_i-x_k)\times p_k]+c_i\} \\ &=\min\{f_j+\sum\limits_{k=j+1}^{i-1}(x_i\times p_k)-\sum\limits_{k=j+1}^{i-1}(x_k\times p_k)\}+c_i \\ &=\min\{f_j+x_i\times\sum\limits_{k=j+1}^{i-1}p_k-\sum\limits_{k=j+1}^{i-1}(x_k\times p_k)\}+c_i \end{aligned} \] 利用前缀和优化:设 \(a\) 为 \(p\) 的前缀和数组,\(b\) 为 \(x_i\times p_i\) 的前缀和数组。
则原式可化为: \[ \begin{aligned} f_i&=\min\{f_j+x_i\times(a_{i-1}-a_j)-(b_{i-1}-b_j)\}+c_i \\ &=\min\{f_j+x_i\times a_{i-1}-x_i\times a_j-b_{i-1}+b_j\}+c_i \\ &=\min\{f_j-x_i\times a_j+b_j\}+x_i\times a_{i-1}-b_{i-1}+c_i \end{aligned} \] 令 \(j\) 优于 \(k\) 。
则有: \[ f_j-x_i\times a_j+b_j<f_k-x_i\times a_k+b_k \\ f_j-f_k+b_j-b_k<x_i\times a_j-x_i\times a_k \\ \dfrac{(f_j+b_j)-(f_k+b_k)}{a_j-a_k}<x_i \]
想感受人生的同学们可以尝试做一下 AcWing 那个版本,非 MLE 即 WA,爽到炸。
#include <cstdio>
#define int long long
const int maxn = 1e6 + 5;
const int LEN = (1 << 20);
int n, L, R;
int f[maxn], x[maxn], p[maxn];
int a[maxn], b[maxn], c[maxn], q[maxn];
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
inline int getup(int j, int k) { return (f[j] + b[j]) - (f[k] + b[k]); }
inline int getdown(int j, int k) { return (a[j]) - (a[k]); }
inline int getDP(int i, int j) { return f[j] - x[i] * a[j] + b[j] + x[i] * a[i - 1] - b[i - 1] + c[i]; }
signed main() {
read(n); L = R = 1;
for (int i = 1; i <= n; ++i) {
read(x[i]); read(p[i]); read(c[i]);
a[i] = a[i - 1] + p[i];
b[i] = b[i - 1] + x[i] * p[i];
}
for (int i = 1; i <= n; ++i) {
while (L < R && getup(q[L + 1], q[L]) <= x[i] * getdown(q[L + 1], q[L]))
++L;
f[i] = getDP(i, q[L]);
while (L < R && getup(i, q[R]) * getdown(q[R], q[R - 1]) <= getdown(i, q[R]) * getup(q[R], q[R - 1]))
--R;
q[++R] = i;
}
printf("%lld", f[n]);
return 0;
}锯木厂选址
和仓库建设很像。
设 \(A_i=\sum\limits_{j=i}^nd_j\),表示第 \(i\) 棵树与山脚的距离;\(B_i=\sum\limits_{j=1}^iw_j\),表示 \(w\) 的前缀和;\(S=\sum\limits_{i=1}^nA_i\times w_i\),表示将所有树全部运到山脚的花费总和。
假设在 \(j\) 处建立第 \(1\) 座锯木厂,在 \(i\) 处建立第 \(2\) 座锯木厂,此时:
- 对于第 \(1\sim j\) 棵树来说,\(S\) 比实际情况多运了 \(A_j\) 的路程;
- 对于第 \(j+1\sim i\) 棵树来说,\(S\) 比实际情况多运了 \(A_i\) 的路程。
将对应的多运的距离与花费相乘的结果,让 \(S\) 将其减去即可。 \[ \begin{aligned} ans&=\min\{S-A_j\times B_j-(B_i-B_j)\times A_i\}\\ &=\min\{A_i\times B_j-A_j\times B_j\}+S-A_i\times B_i \end{aligned} \] 令 \(j<k\) 且 \(j\) 优于 \(k\),则有: \[ \begin{aligned} A_i\times B_j-A_j\times B_j&<A_i\times B_k-A_k\times B_k\\ -A_j\times B_j+A_k\times B_k&<-A_i\times B_j+A_i\times B_k\\ \dfrac{-A_j\times B_j+A_k\times B_k}{-B_j+B_k}&<A_i\\ \dfrac{A_j\times B_j-A_k\times B_k}{B_j-B_k}&<A_i\\ \end{aligned} \] 其中,\(A_i\) 具有单调性,可以直接套板子。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define int long long
const int inf = 1e18;
const int maxn = 1e6 + 5;
const int LEN = (1 << 20);
int w[maxn], d[maxn];
int n, L, R, s, ans = inf;
int q[maxn], a[maxn], b[maxn];
inline int min(int x, int y) { return x < y ? x : y; }
inline int getDP(int i, int j) {
return s - a[j] * b[j] - (b[i] - b[j]) * a[i];
}
inline int getup(int j, int k) {
return a[j] * b[j] - a[k] * b[k];
}
inline int getdown(int j, int k) {
return b[j] - b[k];
}
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
signed main() {
read(n);
L = R = 1;
for (int i = 1; i <= n; ++i) {
read(w[i]), read(d[i]);
b[i] = b[i - 1] + w[i];
}
for (int i = n; i; --i) {
a[i] = a[i + 1] + d[i];
s += a[i] * w[i];
}
for (int i = 1; i <= n; ++i) {
while (L < R && getup(q[L + 1], q[L]) >= a[i] * getdown(q[L + 1], q[L]))
++L;
ans = min(ans, getDP(i, q[L]));
while (L < R && getup(i, q[R]) * getdown(q[R], q[R - 1]) >= getup(q[R], q[R - 1]) * getdown(i, q[R]))
--R;
q[++R] = i;
}
printf("%lld", ans);
return 0;
}Cats Transport
经验:洛谷的题面比蓝书和 AcWing 上的标准多了,蓝书的题意不清。
研究表明,边猛灌养乐多边看蓝书有助于理解。
这道题难在推式子。不然还能难在哪里
设 \(A_i\) 表示要接到第 \(i\) 只猫的最早出发时间,也就是说,在此时出发,猫 \(i\) 的等待时间为 \(0\)。
即 \(A_i=T_i-\sum\limits_{j=1}^{H_i}D_j\),也就是出发时间=到达时间-经过时间。
此时我们可以把其他所有因素去掉,题意转换为:
已知在 \(\geqslant A_i\) 的时刻出发可以接到猫 \(i\) ,在 \(P\) 次出发次数的限制内接到所有猫,猫的等待时间之和最小是多少?
假设饲养员在 \(t\) 时刻出发,猫 \(i\) 的等待时间就是 \(t-A_i\)。
对 \(A_i\) 从小到大排序。
显然,一次接一段连续的猫,花费自然是最小的。
若我们要接 \([k+1,j]\) 范围内的猫,它们的等待时间之和就是: \[ \begin{aligned} \sum\limits_{p=k+1}^{j}(A_j-A_p)&=[j-(k+1)+1]A_j-\sum\limits_{p=k+1}^{j}A_p \\ &=(j-k)\times A_j-(S_j-S_k) \\ &=j\times A_j-k\times A_j-S_j+S_k \end{aligned} \] 其中 \(S\) 为 \(A\) 的前缀和。
设 \(f_{i,j}\) 表示前 \(i\) 个饲养员带走前 \(j\) 只猫的最小花费。
则有: \[ \begin{aligned} f_{i,j}&=\min\{f_{i-1,k}+j\times A_j-k\times A_j-S_j+S_k\} \\ &=\min\{f_{i-1,k}-A_j\times k+S_k\}+A_j\times j-S_j \end{aligned} \]
我们将循环地枚举每个饲养员的循环变量 \(i\) 看做常量。
令 \(x\) 优于 \(y\),则有: \[ f_{i-1,x}-A_j\times x+S_x<f_{i-1,y}-A_j\times y+S_y \\ \dfrac{(f_{i-1,x}+S_x)-(f_{i-1,y+S_y})}{x-y}<A_j \] 注意事项
\(f\) 初始化为极大值。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define int long long
const int maxp = 105;
const int maxn = 1e5 + 5;
const int LEN = (1 << 20);
int f[maxp][maxn];
int n, m, p, L, R, t, h;
int q[maxn], a[maxn], d[maxn], s[maxn];
inline int getDP(int i, int j, int k) {
return f[i - 1][k] + (j - k) * a[j] - (s[j] - s[k]);
}
inline int getup(int i, int j, int k) {
return (f[i - 1][j] + s[j]) - (f[i - 1][k] + s[k]);
}
inline int getdown(int j, int k) {
return (j) - (k);
}
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
signed main() {
read(n); read(m); read(p);
memset(f, 0x3f, sizeof (f));
for (int i = 2; i <= n; ++i)
read(d[i]), d[i] += d[i - 1];
for (int i = 1; i <= m; ++i) {
read(h); read(t);
a[i] = t - d[h];
}
std::sort(a + 1, a + m + 1);
for (int i = 1; i <= m; ++i)
s[i] = s[i - 1] + a[i];
f[0][0] = 0;
for (int i = 1; i <= p; ++i) {
L = R = 1;
for (int j = 1; j <= m; ++j) {
while (L < R && getup(i, q[L + 1], q[L]) <= a[j] * getdown(q[L + 1], q[L]))
++L;
f[i][j] = getDP(i, j, q[L]);
while (L < R && getup(i, j, q[R]) * getdown(q[R], q[R - 1]) <= getup(i, q[R], q[R - 1]) * getdown(j, q[R]))
--R;
q[++R] = j;
}
}
printf("%lld", f[p][m]);
return 0;
}特别行动队
直接推式子。 \[ \begin{aligned} f_i&=\max\{f_j+a\times(s_i-s_j)^2+b\times(s_i-s_j)+c\ \}\\ &=\max\{f_j+a\times({s_i}^2-2\times s_i\times s_j+{s_j}^2)+b\times s_i-b\times s_j\ \}+c\\ &=\max\{f_j+a\times{s_i}^2-2\times a\times s_i\times s_j+a\times{s_j}^2-b\times s_j\ \}+b\times s_i+c\\ &=\max\{f_j-2\times a\times s_i\times s_j+a\times{s_j}^2-b\times s_j\ \}+a\times{s_i}^2+b\times s_i+c\\ \end{aligned} \] 令 \(j\) 优于 \(k\),则有: \[ \begin{aligned} f_j-2\times a\times s_i\times s_j+a\times{s_j}^2-b\times s_j&>f_k-2\times a\times s_i\times s_k+a\times{s_k}^2-b\times s_k\\ (f_j+a\times{s_j}^2-b\times s_j)-(f_k+a\times{s_k}^2-b\times s_k)&>(2\times a\times s_i\times s_j)-(2\times a\times s_i\times s_k)\\ \dfrac{(f_j+a\times{s_j}^2-b\times s_j)-(f_k+a\times{s_k}^2-b\times s_k)}{(2\times a\times s_j) - (2\times a\times s_k)}&>s_i\\ \end{aligned} \] 我们发现中间的符号是 \(>\)。
所以我们在弹队头的时候,要把判断条件中的符号反过来。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define int long long
const int maxn = 1e6 + 5;
const int LEN = (1 << 20);
int n, L, R, a, b ,c;
int q[maxn], s[maxn], f[maxn];
inline int getDP(int i, int j) {
return f[j] + a * (s[i] - s[j]) * (s[i] - s[j]) + b * (s[i] - s[j]) + c;
}
inline int getup(int j, int k) {
return (f[j] + a * s[j] * s[j] - b * s[j]) - (f[k] + a * s[k] * s[k] - b * s[k]);
}
inline int getdown(int j, int k) {
return (2 * a * s[j]) - (2 * a * s[k]);
}
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
signed main() {
read(n); read(a); read(b); read(c);
L = R = 1;
for (int i = 1; i <= n; ++i) {
read(s[i]), s[i] += s[i - 1];
while (L < R && getup(q[L + 1], q[L]) >= s[i] * getdown(q[L + 1], q[L]))
++L;
f[i] = getDP(i, q[L]);
while (L < R && getup(i, q[R]) * getdown(q[R], q[R - 1]) <= getup(q[R], q[R - 1]) * getdown(i, q[R]))
--R;
q[++R] = i;
}
printf("%lld", f[n]);
return 0;
}征途
明显,不化掉 \(v\times m^2\) 就无法进行优化。
设 \(x\) 为当前休息站点与上一休息站点的距离, \(x_0\) 为 \(x_1\sim x_n\) 的平均数,\(S\) 为 \(x\) 的前缀和。 \[ \begin{aligned} V\times m^2&=[(x_1-x_0)^2+(x_2-x_0)^2+\cdots+(x_m-x_0)^2]\times m \\ &=m\times \sum\limits_{i=1}^{m}{x_i}^2+(m\times {x_0})^2-2\times (x_0\times m)\times \sum\limits_{i=1}^{m}x_i \\ &=m\times \sum\limits_{i=1}^{m}{x_i}^2+{S_m}^2-2\times{S_m}^2 \\ &=m\times \sum\limits_{i=1}^{m}{x_i}^2-{S_m}^2 \end{aligned} \]
其中 \(S_m\) 是一个定值(即输入所有路的长度和)。
唯一需要计算的,就是 \(\sum\limits_{i=1}^{m}{x_i}^{2}\),所以我们就来 DP 它。
设 \(a\) 为输入道路长度的前缀和数组,\(f_{i,j}\) 表示第 \(i\) 次休息在 \(j\) 处时 \(\min\{\sum\limits_{k=1}^{i}{x_k}^2\}\) 的值,则有: \[ \begin{aligned} f_{i,j}&=\min\{f_{i-1,j}+(a_i-a_j)^2\} \\ &=\min\{f_{i-1,j}+{a_i}^2-2\times a_i\times a_j+{a_j}^2\} \end{aligned} \] 令 \(j\) 优于 \(k\),则有: \[ f_{i-1,j}-2\times a_i\times a_j+{a_j}^2<f_{i-1,k}-2\times a_i\times a_k+{a_k}^2 \\ f_{i-1,j}-f_{i-1,k}+{a_j}^2-{a_k}^2<2\times a_i\times(a_j-a_k) \\ \dfrac{f_{i-1,j}-f_{i-1,k}+{a_j}^2-{a_k}^2}{2\times(a_j-a_k)}<a_i \]
初始化。
将 \(f\) 初始化为极大值。
在 AcWing 上将 memset 改为初始化 f[0][i] = a[i] * a[i] 就可以过了,不然会 MLE,也许是因为没开滚动。(本来也用不着滚
#include <cstdio>
#define int long long
const int inf = 1e18;
const int maxn = 3005;
const int LEN = (1 << 20);
int f[maxn][maxn];
int a[maxn], q[maxn];
int n, m, L, R, ans = inf;
#ifdef ONLINE_JUDGE
inline int nec(void) {
static char buf[LEN], *p = buf, *e = buf;
if (p == e) {
e = buf + fread(buf, 1, LEN, stdin);
if (e == buf) return EOF; p = buf;
}
return *p++;
}
#else
#define nec getchar
#endif
inline bool read(int &x) {
char ch = nec();
bool f = 0; x = 0;
while (ch < '0' || ch > '9') {
if (ch == EOF) return 0;
if (ch == '-') f = 1;
ch = nec();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = nec();
}
if (f) x = -x;
return 1;
}
inline int min(int x, int y) { return x < y ? x : y; }
int getDP(int i, int j, int k) {
return f[k - 1][j] + (a[i] - a[j]) * (a[i] - a[j]);
}
int getup(int j, int k, int i) {
return f[i - 1][j] - f[i - 1][k] + a[j] * a[j] - a[k] * a[k];
}
int getdown(int j, int k) {
return (a[j] - a[k]) << 1;
}
signed main(){
read(n); read(m);
for (int i = 1; i <= n; ++i) {
read(a[i]);
a[i] += a[i - 1];
f[0][i] = a[i] * a[i];
}
for (int i = 1; i < m; ++i) {
L = R = 1; q[L] = i;
for (int j = i; j <= n; ++j) {
while (L < R && getup(q[L + 1], q[L], i) <= a[j] * getdown(q[L + 1], q[L]))
++L;
f[i][j] = getDP(j, q[L], i);
while (L < R && getup(i, q[R], i) * getdown(q[R], q[R - 1]) <= getup(q[R], q[R - 1], i) * getdown(i, q[R]))
--R;
q[++R] = j;
}
}
printf("%lld",m * f[m - 1][n] - a[n] * a[n]);
return 0;
}柠檬
是边写这篇题解边做的(
题意:
有一个含有 \(n\) 个元素的序列 \(s\)。将这个序列分成连续的若干段,定义每一段的价值为「在这一段当中任选某个元素的个数的平方再乘上这个元素」的最大值。求将 \(s\) 划分后的最大价值。
不难想到分成的每一段首尾元素必须相等。
比如有这样一个序列 \(x,a_1,a_2,a_3,\cdots,a_k,x,y\) 。假设我们求的是这一段包含 \(x\) 的个数的平方,那么完全可以将 \(y\) 从这一段中分离,单独为一段,明显更优。
而其他所有情况都是这种情况的拓展。
于是得到式子: \[ f_i=\max\{f_{j-1}+s_i\times(cnt_i-cnt_j+1)^2\} \] 其中 \(cnt_i\) 为 \(s_i\) 已经出现了多少次。
然后就是套路。 \[ \begin{aligned} f_i&=\max\{f_{j-1}+s_i\times({cnt_i}^2+{cnt_j}^2-2\times cnt_i\times cnt_j+2\times cnt_i-2\times cnt_j+1)\} \\ &=\max\{f_{j-1}+s_i\times{cnt_i}^2+s_i\times{cnt_j}^2-2\times s_i\times cnt_i\times cnt_j+2\times s_i\times cnt_i-2\times s_i\times cnt_j+s_i\} \\ &=\max\{f_{j-1}+s_i\times {cnt_j}^2-2\times s_i\times cnt_i\times cnt_j-2\times s_i\times cnt_j\}+s_i\times {cnt_i}^2+2\times s_i\times cnt_i+s_i \end{aligned} \] 这次不是 \(\min\),而是 \(\max\),我们还能像以前那样推吗?
不急,我们先按以前的方法试试,见机行事。
令 \(j\) 优于 \(k\),则有: \[ f_{j-1}+s_i\times {cnt_j}^2-2\times s_i\times cnt_i\times cnt_j-2\times s_i\times cnt_j>f_{k-1}+s_i\times {cnt_k}^2-2\times s_i\times cnt_i\times cnt_k-2\times s_i\times cnt_k \] 暴力搞不出来,因为那个 \(s_i\) 乘上的平方项。
那我们想一个办法,把 \(s_i\) 给灭掉就行了。
既然我们已知一段的首尾元素必须相等,那不就说明 \(s_i,s_j,s_k\) 可以相互替换吗?
继续搞。 \[ f_{j-1}+s_j\times {cnt_j}^2-2\times s_i\times cnt_i\times cnt_j-2\times s_j\times cnt_j>f_{k-1}+s_k\times {cnt_k}^2-2\times s_i\times cnt_i\times cnt_k-2\times s_k\times cnt_k \\ f_{j-1}-f_{k-1}+s_j\times {cnt_j}^2-s_k\times {cnt_k}^2-2\times s_j\times cnt_j+2\times s_k\times cnt_k>2\times s_i\times cnt_i\times cnt_j-2\times s_i\times cnt_i\times cnt_k \\ \dfrac{f_{j-1}-f_{k-1}+s_j\times {cnt_j}^2-s_k\times {cnt_k}^2-2\times s_j\times cnt_j+2\times s_k\times cnt_k}{cnt_j-cnt_k}>2\times s_i\times cnt_i \]
这里的符号变成 \(>\) 了。
易得,这里要维护的是一个斜率单调递减的上凸包最优解序列。
因为 \(s_i\) 必须与 \(s_j,s_k\) 相同,明显要针对每个 \(s_i\) 维护不同的最优解序列,在每次对应的序列中计算。
维护的斜率单调递减,而对于每一个相等的 \(s_i\), \(2\times s_i\times cnt_i\) 一定是单调递增的,导致了这个序列大概长这个样子:斜率单调递减,但末尾的最小的斜率仍大于 \(2\times s_i\times cnt_i\)。
单调栈可以自行研究,因为作者瞄了一眼时间发现已经是明天了。(什
#include<cstdio>
#include<vector>
using namespace std;
#define int long long
#define top q[x].size() - 1
const int maxn = 1e5 + 5;
const int maxm = 1e4 + 5;
int n;
vector<int> q[maxm]; // 不用 vector 会 MLE
int f[maxn], s[maxn];
int cnt[maxn], tot[maxm];
int getDP(int i,int j){
return f[j-1]+(cnt[i]-cnt[j]+1)*(cnt[i]-cnt[j]+1)*s[i];
}
int getup(int j,int k){
return f[j-1]-f[k-1]+s[j]*cnt[j]*cnt[j]-s[k]*cnt[k]*cnt[k]-2*s[j]*cnt[j]+2*s[k]*cnt[k];
}
int getdown(int j,int k){
return cnt[j]-cnt[k];
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;++i){
scanf("%lld",&s[i]);
cnt[i]=++tot[s[i]];
}
for(int i=1;i<=n;++i){
int x=s[i];
while(q[x].size()>=2&&getup(q[x][top-1],i)*getdown(q[x][top-1],q[x][top])>=getup(q[x][top-1],q[x][top])*getdown(q[x][top-1],i))
q[x].pop_back();
q[x].push_back(i);
while(q[x].size()>=2&&getDP(i,q[x][top])<=getDP(i,q[x][top-1]))
q[x].pop_back();
f[i]=getDP(i,q[x][top]);
}
printf("%lld",f[n]);
return 0;
}总结
总结斜优的步骤:
- 推 DP 式子
- 对式子进行巧妙的优化,使其易于化简
- 假设 \(j\) 优于 \(k\),将式子化成 \(\dfrac{(j)-(k)}{(j)-(k)}> \text{or} <x\) 的形式
- 单调队列或单调栈优化